vectorDB 直观接触
简单的向量数据库可以参见: https://vectordb.com/ :
import sys
from vectordb import Memory
print(sys.version)
print(sys.platform)
memory = Memory()
memory.save("Hello world")
memory.save(
["apples are red", "oranges are orange"],
[{"url": "https://apples.com"}, {"url": "https://oranges.com"}],
)
# Search for top n relevant results, automatically using embeddings
query = "hello"
results = memory.search(query, top_n = 1)
print(results)不过在中国大陆大概会遇到以下报错:HTTPSConnectionPool(host='huggingface.co', port=443)
先看理论吧。
NLP(Natural Language processing) 与Vector
什么是NLP
自然语言处理(NLP)专注让计算机能够以有意义和有价值的方式理解和响应人类语言。简单来说,我们可以构建一个包含所有句子的词典来实现这一目标,但这有些不切实际,因为人类语言中用于构成句子的单词组合无穷无尽。而且口语中还有口音、多样的同义词汇、错误发音或句中省略单词等等情况,就很复杂,所以诞生了NLP这个学科专门研究如何让计算机处理人类语言。
GPT 与 NLP的关系
NLP 的初始步骤通常是文本数据的预处理。预处理的工作包括
- 分段:将句子分解为组成词
- token 化:将文本分割为单个单词或 token
- 停用词:去除像停用词和普通词如“the”或“is”这样不携带太多含义的标点
- 应用词干提取:为给定标记推导词干
- 词形还原:从字典中获取标记的含义以得到根源以将单词还原为其基本形式
预处理之后的文本会被拿去训练。在大型数据集上接受训练以执行特定NLP任务的深度学习模型被称为 NLP 的预训练模型(PTM,Pre-trained Model),它们可以通过避免从头开始训练新模型来帮助下游 NLP 任务。
GPT-Generative Pre-trained Transformer,即经过预训练的Transformer模型,就是一个 PTM 。和以往其他PTM不一样的是,GPT3.5已经拥有1750亿的参数,而其功能简单解释就是不断预测输入后的下一个单词。并且虽然我们已经用了很久GPT,但现在GPT仍然是一个黑盒,业界还不知道为什么GPT可以做到它涌现的能力。
值得一提的是,llama-2-70b 就是文件系统上的两个文件,一个参数文件和一个运行这些参数的二进制代码。文件大小也就140G左右(700亿参数,每个参数2byte)1。
NLP 的应用
后来人们的目标不仅仅是处理自然语言,而是处理各种非结构化信息,比如图像、音乐乃至商品描述的推荐。
- 聊天机器人
- 图像搜索
- 文本搜索
- 商品推荐
- 音乐推荐
- 语言翻译服务
- 情感分析工具
- 内容生成
传统的数据库,无论是关系型、Nosql 或者 NewSql数据库,将图片转为二进制到存入都很简单,但是我们没有办法直接以图搜图。当然,如果我们是想要以文搜文,自然语言文本(字符串)也可以正则模糊匹配(%),或者借由2.2.2.5. LevenShtein自动机 ,但如果输入是一句话呢?
NLP尤其是生成型AI引发的热潮促使开发者寻找一种简便的方法来存储与查询各种非结构化信息的输出。如果将那些不可以比较的数据转换成为向量,且这些向量的分布和距离可以反映出实体的关系,那么就可以通过比较向量进行检索,也就可以实现图搜图、文搜文的功能。而通过 AI/ML 算法,就可以实现向量化(vector embeddings)。例如可以将不同尺寸、不同内容的图片映射成为由像素值组成的同一个空间内的向量,然后在图像搜索中,当用户输入一张图片进行搜索时,可以将其转换为一个向量,并进行相似度搜索,以便找到与输入图片最相似的图片。同样在推荐系统中,将商品、商品和用户的关系都用向量表示,继而也可以通过相似度搜索来推荐相似、相关的物品给用户。
举个形象的例子,如果我们把每一个单词看作向量,king减queen之差与man与woman之差应该是近似的,都代表着性别的差异。
import matplotlib.pyplot as plt
import logging
logging.basicConfig(level=logging.INFO)
class Point:
"""表示一个点的类"""
def __init__(self, x, y, z, label):
self.x = x
self.y = y
self.z = z
self.label = label
def plot(self, ax):
"""在给定的轴上绘制这个点"""
ax.scatter(self.x, self.y, self.z)
ax.text(self.x, self.y, self.z, self.label)
logging.info("Point plotted: " + self.label)
def create_figure_and_axes():
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
return fig, ax
def set_axes_labels(ax):
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
def set_axes_origin(ax):
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
def hide_axes_lines(ax):
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
def add_axes_arrows(ax):
ax.quiver(0, 0, 0, 1, 0, 0, length=5, normalize=True)
ax.quiver(0, 0, 0, 0, 1, 0, length=5, normalize=True)
ax.quiver(0, 0, 0, 0, 0, 1, length=5, normalize=True)
def finalize_plot(ax):
"""完成图形设置并显示"""
ax.set_xlim([0, 10])
ax.set_ylim([0, 10])
ax.set_zlim([0, 10])
plt.show()
logging.info("Plot displayed.")
# 使用这些函数
fig, ax = create_figure_and_axes()
set_axes_labels(ax)
set_axes_origin(ax)
hide_axes_lines(ax)
add_axes_arrows(ax)
logging.info("Axes set up complete.")
x = [5, 4, 8, 9]
y = [5, 4, 8, 9]
z = [5, 4, 8, 9]
labels = ['King', 'Queen', 'Man', 'Woman']
for i in range(4):
point = Point(x[i], y[i], z[i], labels[i])
point.plot(ax)
finalize_plot(ax)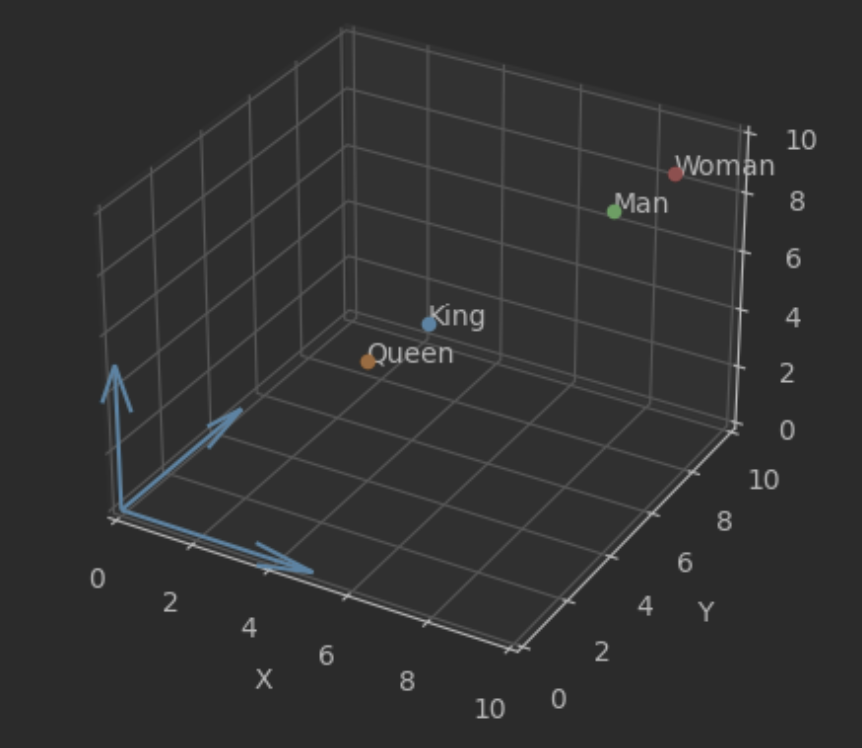
A I时代的JSON-Vector
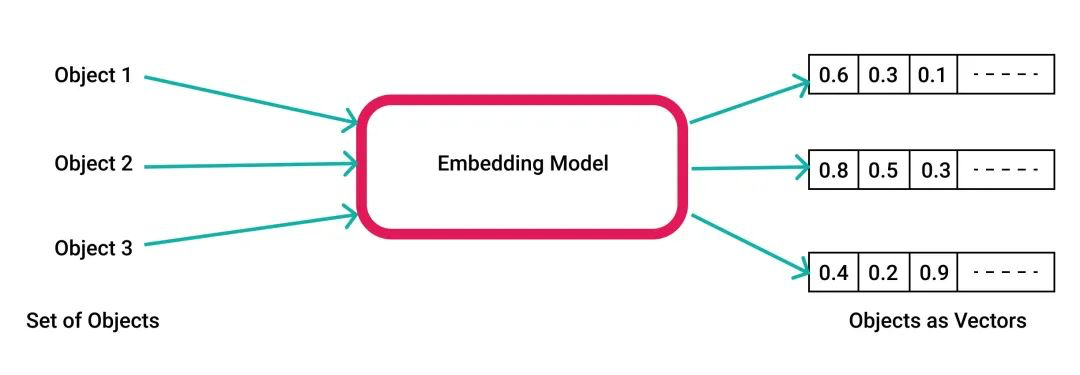
不过向量作为一种数学概念 —— 浮点数数组已经存在数百年了。借由 AI/ML 算法可以将“真实世界”的结构(文本、图像、音频、视频)都用向量的形式表示,并对其存储、查询。这种“通用性”使得 向量成为了AI 时代的JSON2。
 向量之间相似度使用距离函数进行衡量:比如欧式距离,或余弦距离,结果通常会按距离排序取 TOP K,即 K 个最为相似的对象(K-NN, k nearest neighbors)。不过载实际应用中,待检索的数据往往是千万甚至亿级,
向量之间相似度使用距离函数进行衡量:比如欧式距离,或余弦距离,结果通常会按距离排序取 TOP K,即 K 个最为相似的对象(K-NN, k nearest neighbors)。不过载实际应用中,待检索的数据往往是千万甚至亿级,KNN的计算量过大。因会降级采用 ANN(Approximate Nearest Neighbor,相似近邻)来快速相似检索。
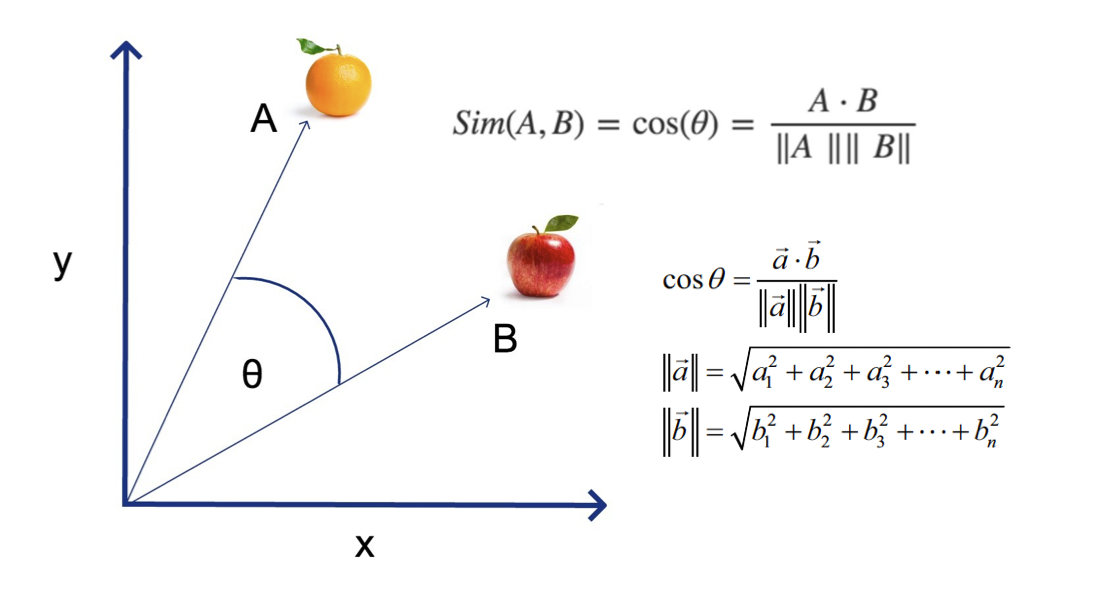
其中余弦距离我们在高中学过:
Vector 的好伙伴VectorDB
虽然向量是浮点数数组,但是因为其巨大的数量(维度)、索引算法、相似度算法,也诞生了专门存储和查询向量的向量数据库,比如 Milvus 和 Pinecone。
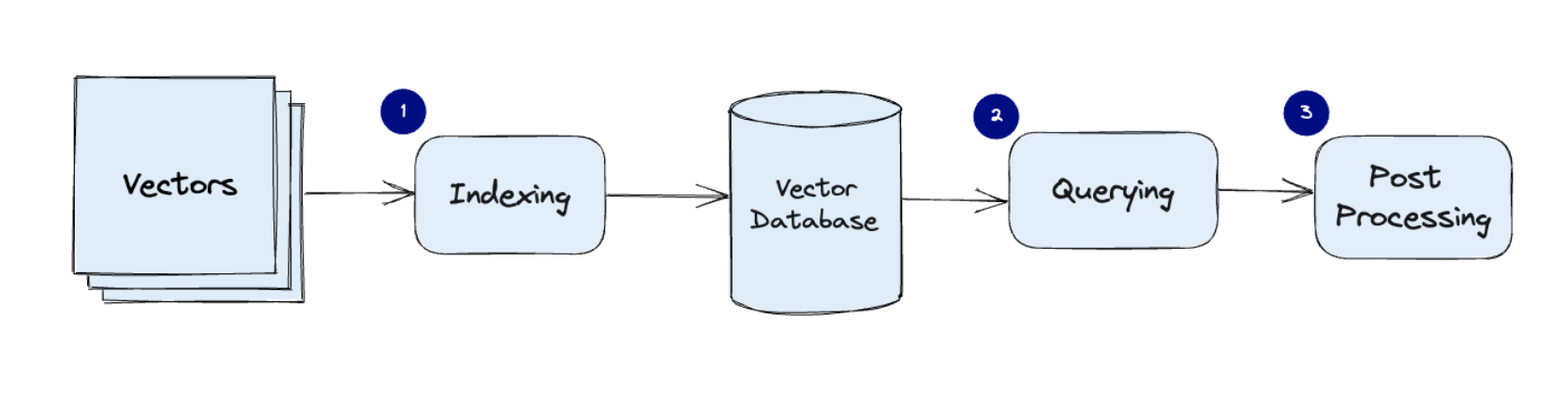
对向量索引
Random Projection(随机投影)
随机投影是一种将高维向量投影到低维空间的技术。它背后的思想是,通过将高维向量投影到一个低维空间,我们可以保留其相似性,同时减少其维度,提高查询性能。例如,在文本数据库中,我们可以使用随机投影将文本向量投影到一个低维空间。这可以使我们更快地找到与查询相似的文本。步骤如下:
- 创建一个随机数矩阵。该矩阵的大小将是我们想要的目标低维值。
- 将输入向量与矩阵相乘。
- 保留输出向量的前几维。
例如,如果我们想将高维空间投影到一个二维的平面,那么我们需要一个 2xn 的随机数矩阵,其中 n 是高维空间的维度。
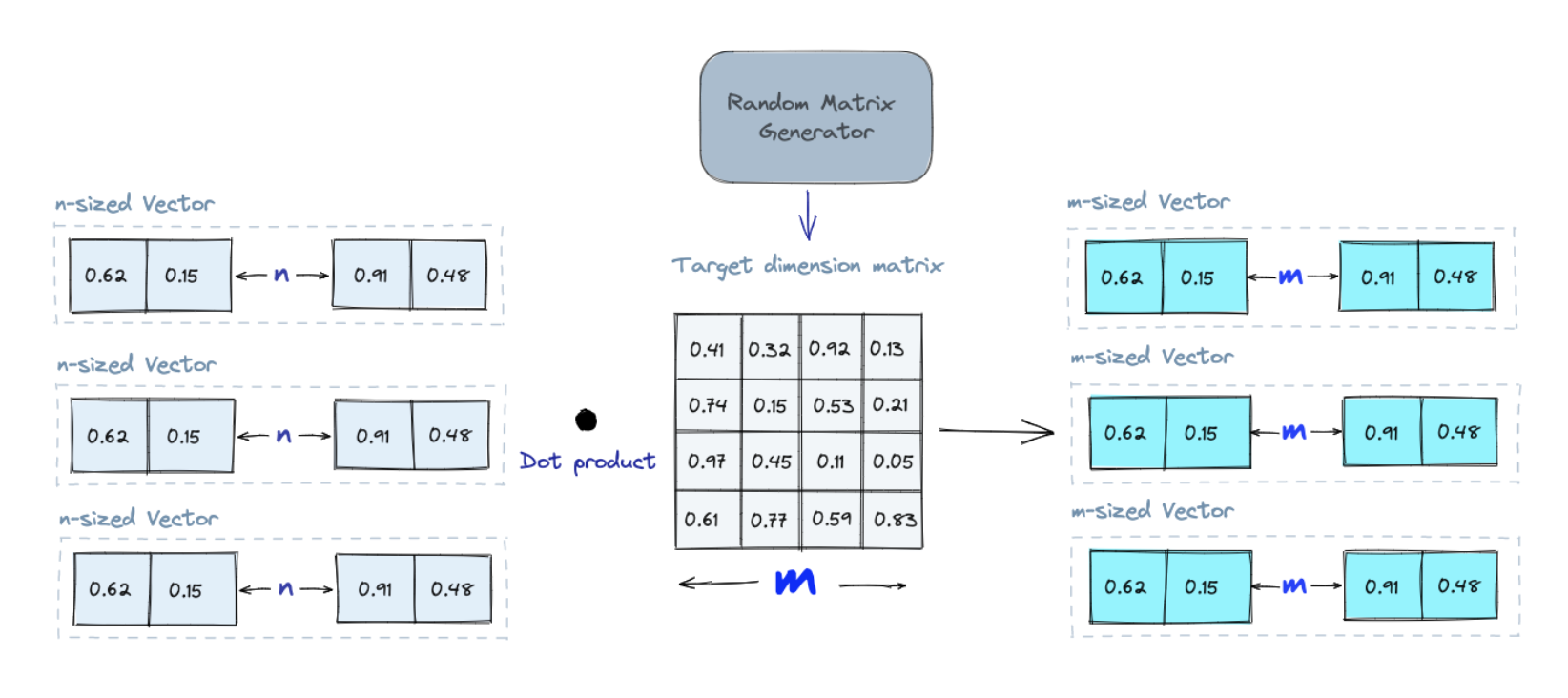
当我们查询时,我们使用相同的投影矩阵将查询向量投影到低维空间上。然后,我们将投影查询向量与数据库中的投影向量进行比较,以找到最近的邻。由于数据的维数降低,搜索过程比搜索整个高维空间要快得多。
Locality-sensitive hashing(局部敏感哈希)
局部敏感哈希 (LSH) 是一种在近似最近邻搜索上下文中建立索引的技术。之所以称为敏感Hash, 是因为选用的Hash函数要满足输入向量相似,输出hash 大小也接近特性。
传统的最近邻查询方法是线性查询。这种方法将查询向量与数据集中的每个向量进行比较,并返回最相似的向量。但对于高维数据集,线性查询太耗时也可能没必要。高维空间中的两个向量可能非常相似,即使它们在空间中相距很远。所以LSH 使用一组hash函数将相似的向量映射到“桶”中,如下所示:
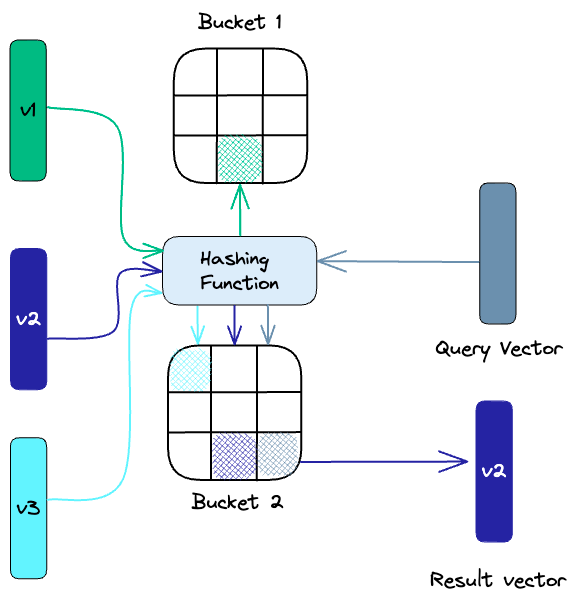
查询的时候再将查询向量hash到特定表,然后与同一表中的其他向量进行比较,以找到最接近的匹配项。这种方法比搜索整个数据集要快得多,因为每个哈希表中的向量比整个空间中的向量少得多。
Inverted Index(倒排索引)
倒排索引和 LSH 思想类似,都是通过聚类方法把整个向量空间划分为子区域,从而缩小检索时的量级。ANN 中的倒排索引每个区域用中心点聚类,在索引构造阶段,向量与中心点比对,将其归属到距离最近的中心点对应的倒排中。

Hierarchical Navigable Small World (HNSW)
上面的相似检索都是基于空间划分的方法,每个向量只会属于某个子区域。它们最大的的问题是为了提高召回率,需要搜索较大空间,导致计算量增加。基于图的方法就可以比较好的解决这一问题3。
图的最朴素的想法是**「邻居的邻居也可能是邻居」**,这样把近邻查找转化为图的遍历。由于图的连通性,可以针对性的搜索部分空间,降低搜索范围。
哈佛大学心理学教授斯坦利·米尔格拉姆于1967年提出
六度分隔理论(Six Degrees of Separation):认为世界上任何互不相识的两人,只需要很少的中间人(6个以内)就能够建立起联系。
基于这种假设,向量顶点之间的关系可以分为两种:
- 同质性:相似的顶点会聚集在一起,相互连接具有邻接边
- 弱连接:在每个顶点上会有一些随机的边随机连接到网络中的顶点上
Navigable small world的原理简单说就是:
通过构建一个small world graph,从图中随机选择一个起始顶点,逐个遍历其邻接节点,选择与目标最近的顶点继续遍历,直到找到最近的顶点。
那怎么构建small world graph?
- **「随机」**向图中逐个插入顶点
- 插入新顶点(new)时,通过计算邻居顶点和待插入顶点的距离来决定下一个要进入的顶点(next)
- 找到与新顶点(new)最近的m个顶点(neighbor)后,将新顶点(new)与它们(neighbor)连接起来形成边
如下图所示,采用随机方法来构造m=3的small world graph:
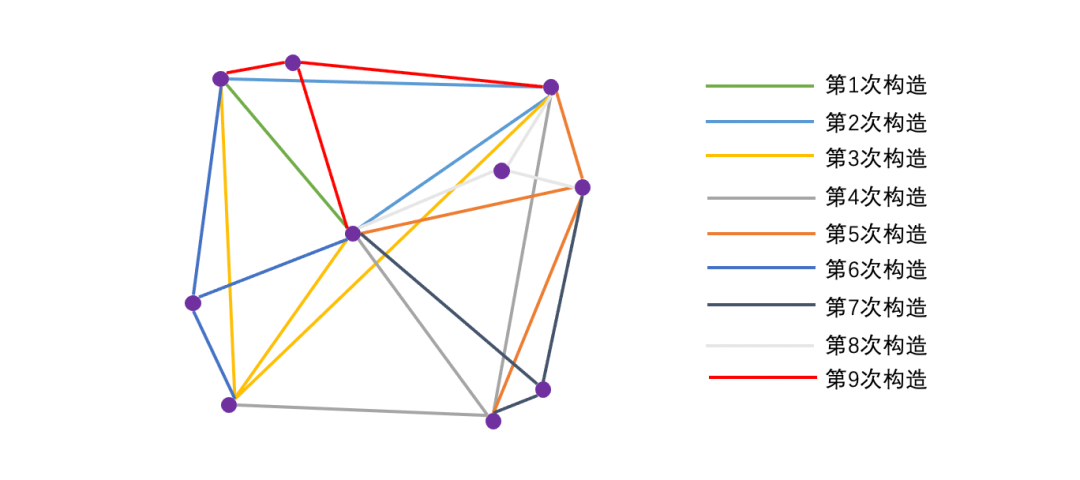
在NSW中,构建图的阶段通过节点的随机插入来引入随机性,构建出一个small world graph,从而实现快速检索。但NSW构造的图并不稳定,节点之间的差异较大:
- 先插入的顶点,其连接的邻居节点,基本都比较远(弱连接属性强)
- 后插入的顶点,其连接的邻居节点,基本都比较近(弱连接属性弱)
- 对于具有聚类效应的点,由于后续插入的点可能都和其建立连接,对应节点的度可能会比较高
如何构造具有更稳定的small world graph呢?HNSW算法就在NSW基础之上引入了分层图的思想,通过对图进行分层,实现由粗到细的检索3,如下图4
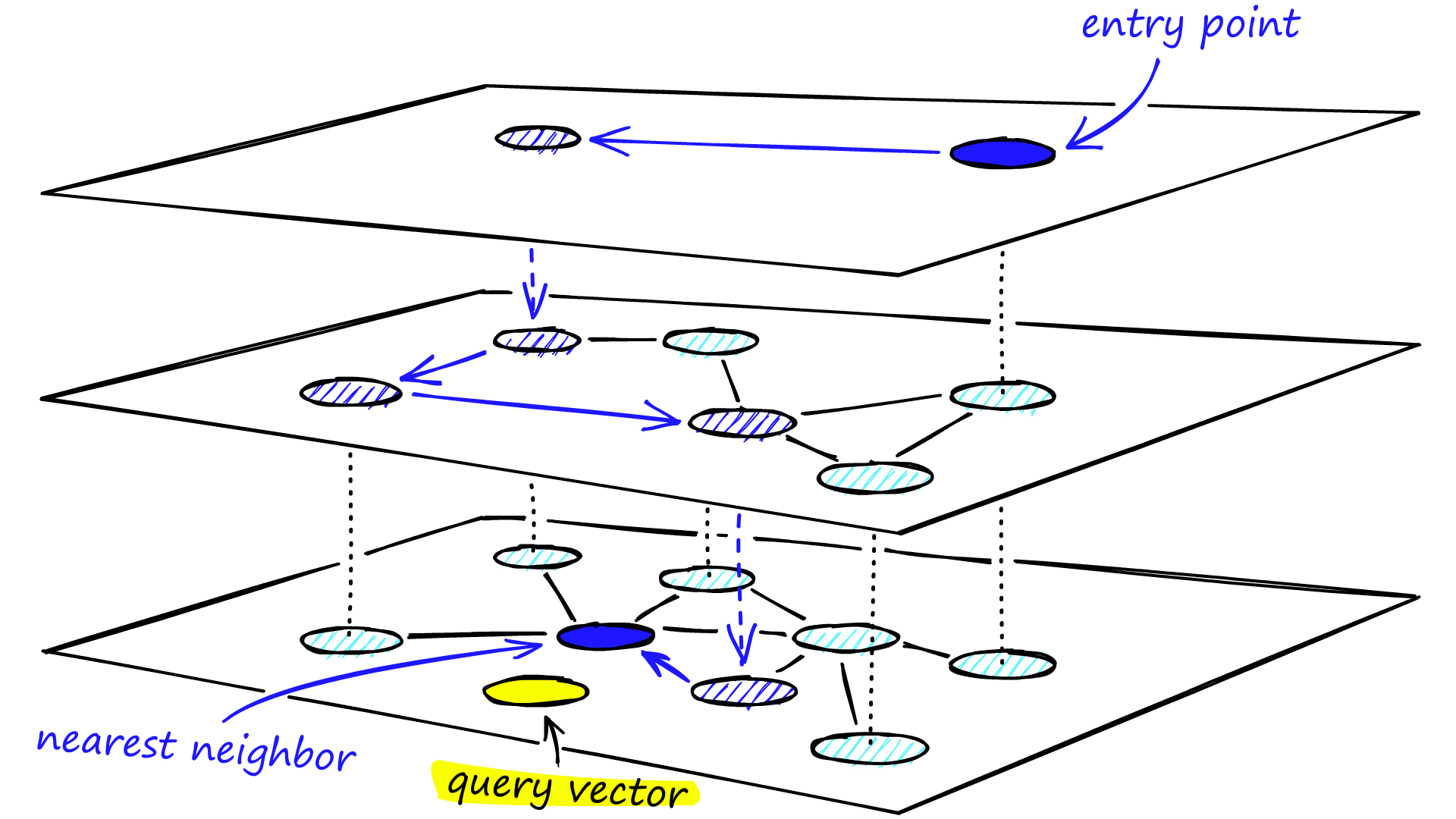
相似度比较指标5
欧几里得距离
欧几里得距离是多维空间中两个向量之间的直线距离。
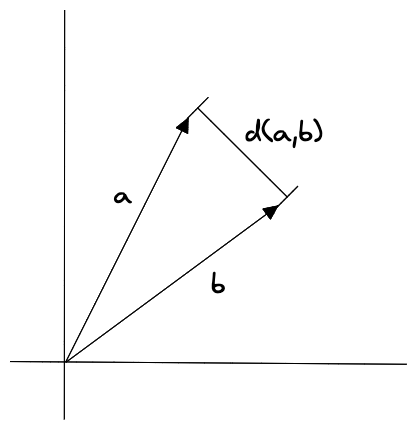
欧几里得距离直接与大小有关,所以与计数或测量的属性有关。假如想推荐与用户以前购买相似的商品,欧几里得距离适合比较购买商品时间的向量相似度。
余弦相似度
测量向量空间中两个向量之间角度的余弦。它的范围从 -1 到 1,其中 1 表示相同的向量,0 表示正交向量,-1 表示截然相反的向量。
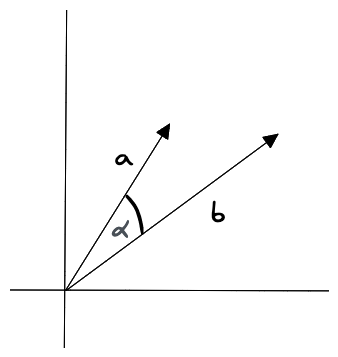
余弦相似度计算时考虑向量的方向,而不考虑向量的大小,所以它适合比较查询内容的整体性质,比如文本分类,但不适合有明确大小比较的场景,图片按温暖分类后,需要用高饱和度图片搜索高饱和度图片。
点积
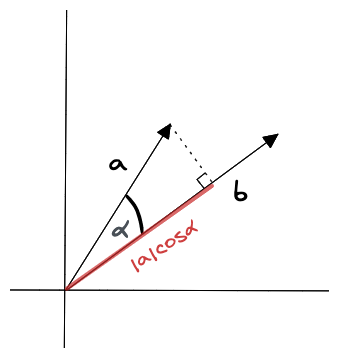
点积是一个标量,同时受向量大小和时间影响,最综合。
上面介绍的是向量之间的相似度比较,扩展到集合(一段文本)层面有更多的度量值。
Jaccard系数、Dice 系数和F1值
Jaccard系数能够量度有限样本集合的相似度,其定义为两个集合A、B交集大小与并集大小之间的比例:
Jaccard系数的取值范围为 [0,1]。当 J(A,B)=1 时,表示 A 和 B 完全相同;当 J(A,B)=0 时,表示 A 和 B 完全不相同。在文本相似度计算中,可以使用 Jaccard系数来计算两个文本的共同词汇量与总词汇量的比例,从而衡量两个文本的相似度。
Jaccard系数 计算简单,不过当两个集合较大时,Jaccard系数容易受集合中随机元素(噪声)干扰。 例如,假设我们有两个集合 A 和 B,其中 A 包含 1000 个元素,B 包含 10000 个元素。如果 A 被 B 完全包括,那么 ∣A∩B∣=1000,∣A∪B∣=11000。Jaccard 系数为:
如果 A 和 B 中存在 10 个噪声元素,那么 ∣A∩B∣=990,∣A∪B∣=10990。Jaccard 系数为:
可以看出,当两个集合较大时,即使两个集合之间只有很小的差异,Jaccard 系数也会有所下降。为了避免这种情况,人们引入Dice 系数:
以及F1 值:
他们简单的优缺点如下:
| 度量方法 | 优点 | 缺点 |
|---|---|---|
| Jaccard 系数 | 计算简单,易于理解 | 对噪声敏感 |
| Dice 系数 | 对噪声不敏感,对不均匀集合敏感 | 计算复杂度较高,对异常值敏感 |
| F1 值 | 兼顾了精度和召回率 | 计算复杂度较高,对零值敏感 |
元数据/标量数据筛选
存储在数据库中的每个向量还包括元数据。除了能够查询相似的向量之外,向量数据库还可以根据元数据查询筛选结果。所谓元数据,就是日期、文本标签、地理标签等。
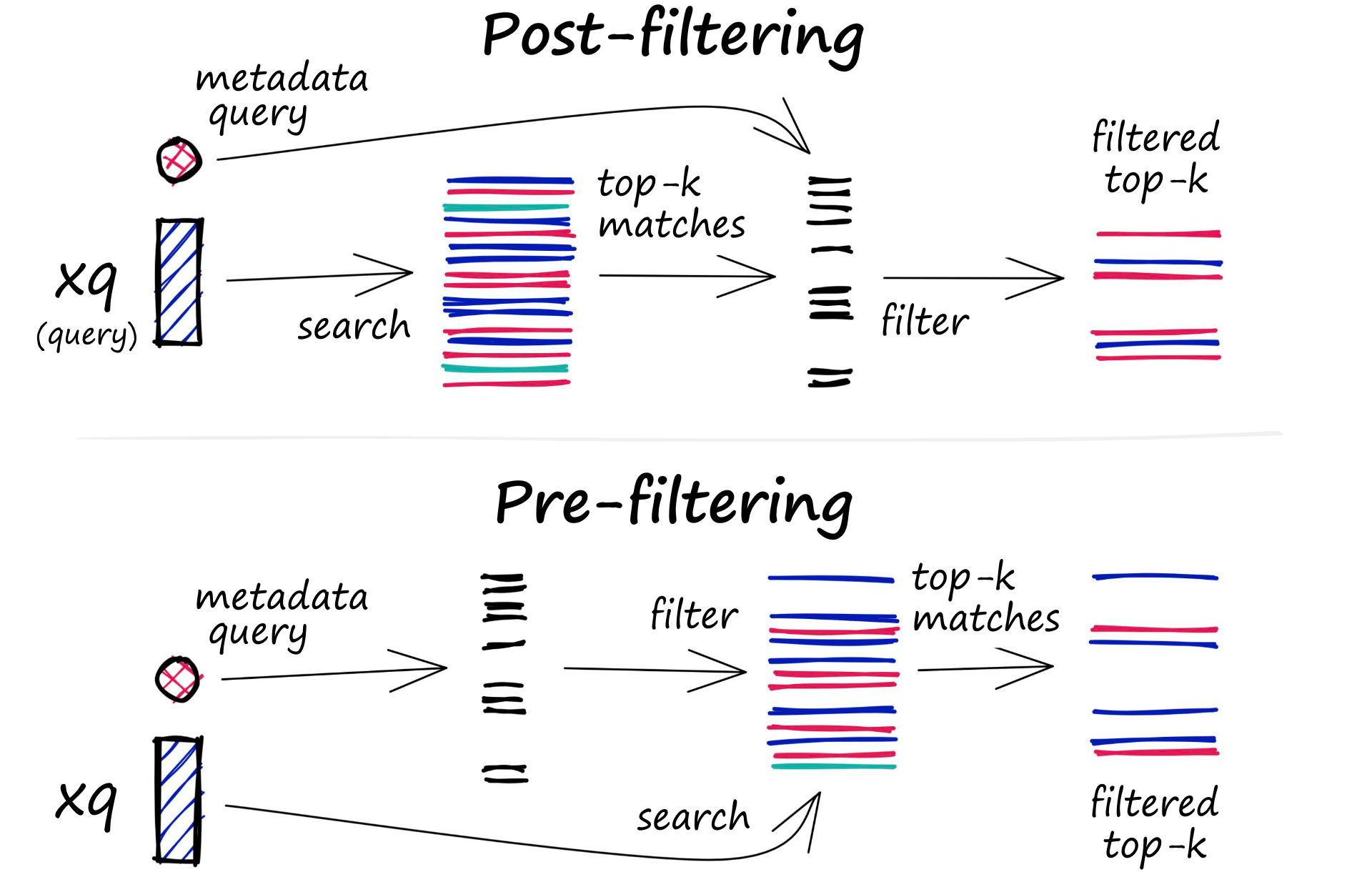
筛选过程可以在向量搜索本身之前或之后执行
- 预过滤:在这种方法中,元数据过滤是在向量搜索之前完成的。虽然这有助于减少搜索空间,但也可能导致系统忽略与元数据筛选条件不匹配的相关结果。此外,由于增加了计算开销,广泛的元数据筛选可能会减慢查询过程。
- 后过滤:在这种方法中,元数据过滤是在向量搜索之后完成的。这有助于确保考虑所有相关结果,但也可能会带来额外的开销并减慢查询过程,因为搜索完成后需要筛选掉不相关的结果。
向量数据库选型
向量本质上就是浮点数数组,对数据库而言相当于多了一个类似JSON的专门存储类型,所以传统的搜索引擎ES或PostgreSQL的向量版或假装向量插件后都可以,甚至用Redis 还更方便。 pg-vector